產品分類
技術文章
氣體組分變化對熱式質量流量計測量精度的影響
發布日期:2022-03-15 來源: 作者: 瀏覽次數:
【導讀】:結合熱式氣體質量流量計的換熱理論與誤差傳遞理論推導出了組分(物性參數)變化對熱式測量影響的定量關系。通過實驗進行測試,組分變化或者組分設定不準確會切實影響到質量流量的測量,且實驗結果與計算分析的附加誤差結果基本一致,使得本文提出的定量關系得以驗證,......
摘要:混合氣體組分變化會造成其物性參數變化,進而對熱式氣體質量流量計測量精度產生影響。結合混合氣體物性參數計算與誤差傳遞理論對氣體組分變化或組分設定不準確時流量測量精度的影響進行了研究與分析,給出了由物性參數變化引起質量流量誤差的定量計算公式。以非常常見的混合氣體———空氣為例進行了實例計算,并采用熱式氣體質量流量計在氣體流量標準裝置上進行實流測試,在300~3000kg/h流量范圍內,空氣組分設定變化1%、5%、10%時對熱式流量測量依次產生0.56%、3.19%、4.94%的誤差,與定量計算公式得到的結果相比具有很好的致性,且在組分變化較大時,由組分變化造成對質量流量的誤差不可忽略,并找到了組分變化不可忽略的臨界值約為3%~5%,為實際應用提供參考。
引言
質量流量能更準確的反映物理過程或化學過程,因此人們一直希望可以對其直接進行測量。然而,大多數流量測量技術是測量體積流量的,在中低壓氣體流量測量技術中,熱式氣體質量流量測量技術幾乎是唯一可行的直接質量流量測量技術。該方法依托于被測氣體的動力粘度、導熱系數、定壓比熱容等物性參數。不同的氣體具有相異的物性參數,因此當氣體組分發生變化或者組分測量不準確時必然會引入質量流量的測量誤差。
1973年,Simpson等[1]采用熱線風速儀對“空氣-He”混合氣體進行了測量研究,研究表明,同一速度下,混合氣體的組分比對測量輸出結果影響十分明顯。2009年,張世榮[2]在熱式氣體質量流量測量及補償算法研究中,利用恒溫差原理的熱式質量流量計,將物性參數分析與經驗公式相結合,提出了一種熱式氣體流量計的組分補償算法。該算法將不同氣體組分引入流量計特性曲線的組分補償系數中,當被測氣體組分改變時,改變上位機的相關系數[3],完成組份補償。根據以往學者的研究,混合氣體的組分變化,會導致熱式氣體質量流量計測量不準確,但是氣體組分變化或者組分設定不準確對熱式氣體質量流量計測量精度影響的定量分析尚未出現相關的報道。
本文針對以上問題展開研究,通過計算分析,推導出由組分變化引起的誤差與質量流量誤差的定量關系,并通過實驗得以驗證。本次研究還得到組分變化影響質量流量誤差的臨界值、優選出適用于熱式氣體質量流量計中計算各相關混合氣體物性參數的方法,均為實際工程應用提供了一定的借鑒。
1熱式氣體質量流量計的基本原理
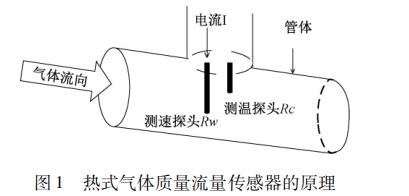
熱式流量測量技術非常早起源于20世紀60年代熱線式傳感器的應用,其作為流量測量技術的一個重要分支,是一種基于熱傳遞原理的直接式質量流量測量方法[4-5],利用流動中的氣體與熱源之間的熱量交換關系直接測量氣體的質量流量。熱式氣體質量流量傳感器的原理如圖1所示。
熱式氣體質量流量傳感器由兩個探頭組成,分別稱為測速探頭Rw和測溫探頭Rc。測溫探頭測量氣體的溫度。測速探頭被加熱到高于被測氣體的溫度,當氣體流過速度探頭,并且達到穩定狀態后,根據牛頓冷卻公式,加熱電功率等于其表面對流換熱的耗散熱量,如式(1)所示,左側是測速探頭加熱的電功率,右側是對流換熱量:
式中:I為測速探頭的供電電流;Rw為速度探頭的電阻值;h為測速探頭對流表面換熱系數;A為測速探頭的外表面積;Tw為測速探頭的溫度;Tc為測溫探頭測量的流體溫度。
式(1)中的傳熱系數h與很多因素相關[6],由Nu定義式為:
Nu=hd/λ(2)
式中:λ為氣體的導熱系數;d為特征尺寸(測速探頭直徑)。
可以將對流換熱過程視為氣體橫掠單管的換熱過程。在該過程有許多的經驗公式[7-8],其中Hilpert提出的氣體橫掠單管的經驗公式應用比較廣泛[9],如式(3)所示。
式中:參數C與n在本次研究中的取值由具體實驗數據擬合得出,參數m根據文獻[6]的經驗值取1/3[6]。Re稱為雷諾數,Re定義為:
Re=ρvd/μ(4)
式中:ρ為氣體的密度;v為氣體的流速;μ為氣體的動力粘度。
式(5)中的Pr稱為普朗特數,其定義為:
式中: Cp 為氣體的定壓比熱容。 聯立公式( 1) ~ ( 5) 可得到測速探頭所測的質量流量 G:
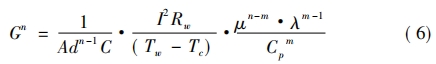
式中:等式左邊為氣體的質量流量,等式右邊分為三個部分:
常值系數:
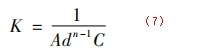
功率溫差比:
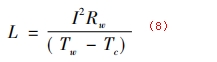
物性參數:

氣體的質量流量除了和功率溫差比相關還與氣體的物性參數相關,涉及到的物性參數包括氣體的動力粘度μ、導熱系數λ、定壓比熱容Cp。氣體的物性參數與氣體自身的物理性質有關,對氣體的質量流量直接產生影響。
2、混合氣體組分對熱式氣體質量流量計的測量誤差影響
2.1、混合氣體組分變化對質量流量測量誤差的計算分析
由上文分析可知,熱式氣體質量流量計的測量結果依賴于被測氣體的物性參數———動力粘度μ、導熱系數λ、定壓比熱容Cp,而不同氣體的物性參數具有顯著差異,表1中列舉了幾種氣體在常壓、20℃條件下的物性參數。
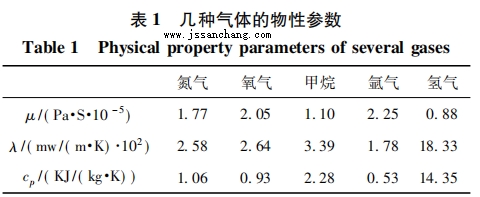
對于單一氣體而言,直接采用其物性參數即可,不會對熱式流量測量帶來影響,但是對于混合氣體而言,當氣體的組分產生變化時,必然會對質量流量的測量產生誤差,即:
混合氣體的組分變化或者組分設定不準確會造成混合氣體的動力粘度μ、導熱系數λ、定壓比熱容Cp產生誤差,進而會影響物性參數Pm,產生Pm的誤差,非常終根據式(6)會對質量流量產生誤差。
首先分析物性參數Pm的誤差對質量流量G誤差影響。質量流量誤差σG根據式(6),結合函數誤差傳遞理論計算得出[10-11]:
結合式(9),進一步利用函數合成標準不確定度理論可以求得Pm的誤差與各物性參數誤差的關系。
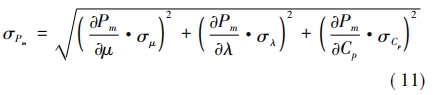
式中:σμ、σλ、σCp、分別表示動力粘度、導熱系數、定壓比熱容的不確定度,在這里也就是誤差。
非常后,聯立式(10)、(11)可以計算出混合氣體物性參數誤差對質量流量誤差的影響。
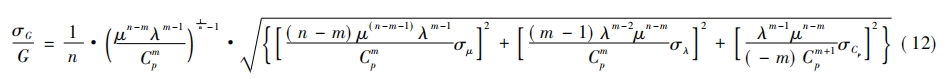
式(12)中的σG/G可以表示出物性參數誤差對質量流量的影響。
2.2混合氣體各物性參數計算方法的分析與選擇
混合氣體的動力粘度μ、導熱系數λ、定壓比熱容Cp分別有各自的多種計算方法。本文對其多種計算方法進行了分析和選擇,為熱式質量流量計在應用上計算混合氣體物性參數提供了一定的參考。
1)混合氣體動力粘度的計算方法
計算混合氣體動力粘度的方法有很多種,應用比較廣泛的為Wilke法[12]。該方法的可靠性已經被大量的計算證明,應衛勇等人在研究含氨混合氣體時應用了Wilke法計算了混合氣體粘度[13],王利恒等[14]組分補償方法的研究中也用此方法計算了混合氣體的粘度,除此之外在文獻[15]中介紹Wilke法比較了17組雙組分混合氣體的數據[15],與實驗值的平均誤差<1%。
Wilke法計算公式如下:
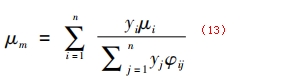
式(13)中,μm為混合氣體的動力粘度,μi為組分i的動力粘度,yi、yj為組分i、j的摩爾分數,φij為結合因子,童景山等對Wilke法氣體混合物粘度方程中的結合因子φij做了改進,使其精度比Wilke法有提升。
本次研究計算混合氣體動力粘度采用童景山法。
2)混合氣體導熱系數的計算方法
迄今為止,提出了許多混合氣體導熱系數的計算式,主要分為Wassiljewa方程法和經驗式法。相比于經驗式法,Wassiljewa方程法具有物理原理作為支撐,計算不依賴于經驗系數,應用更廣泛。
Wassiljewa方程計算混合氣體的導熱系數:
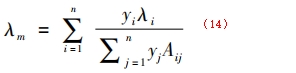
式中:λm為混合氣體的導熱系數;λi為組分i的導熱系數;Aij為結合因子。
關于結合因子Aij的計算方法中,童景山法計算的結合因子誤差相對非常小,結合因子Aij同求粘度過程中童景山法的結合因子φij相同。本次研究計算混合氣體的導熱系數采用童景山法。
3)混合氣體定壓比熱容的計算方法
混合氣體定壓比熱容的計算方法較為統一[16-17],在理論上和實際應用上都采用單一氣體的定壓比熱容與各組分氣體的摩爾分數計算:
式中:Cpm、Cpi為混合氣體的定壓比熱容和組分i的定壓比熱容。
2.3混合氣體組分變化對質量流量測量誤差的實例分析
結合以上對混合氣體物性參數的計算方法,式(13)~(15),及式(12),分析組分變化對典型混合氣體—空氣進行質量流量測量誤差的影響。
空氣可以認為是79%的N2和21%的O2組成的混合氣體。將空氣的組分設定修改為78%N2+22%O2、74%N2+26%O2和69%N2+31%O2,即組分變化分別為1%、5%和10%,分析其對質量流量的影響。
計算的工況條件為20℃、常壓,混合氣體的質量流量G=1000kg/h,可計算出其組分設定不同對質量流量的誤差影響,計算結果如表2所示。
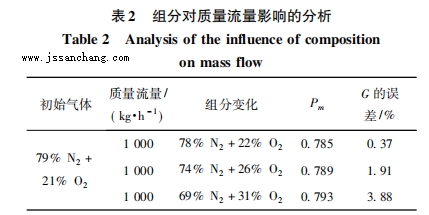
從上述分析計算可知,混合氣體的組分改變,會直接影響混合氣體的物性參數Pm,進而影響質量流量產生誤差。
3實驗測試與結果分析
3.1實驗測試
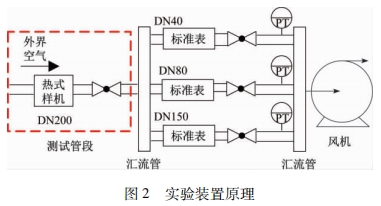
實驗測試所用裝置是在天津大學流量實驗室的氣體流量實驗裝置。實驗裝置采用微負壓法,通過調節風機的頻率來調節氣體流量。標準表由多路并聯的渦輪流量計組成,精度等級為1級,口徑分別為40mm、80mm、150mm。實驗裝置原理如圖2所示。
熱式氣體質量流量計樣機如圖3(a)所示,內部有測速探頭和測溫探頭,詳細的結構如圖3(b)所示。該樣機信號線外接相應的采集電路,如圖3(c)所示,圖的左側為計算采集電路[18-19]。樣機與計算采集電路結構經過多次空氣的實流測試,其與標準表的測量誤差滿足國家JJG1132-2017《熱式氣體質量流量計檢定規程》中的2級的準確度等級,其量程范圍為10~3000kg/h,量程比達300∶1,根據檢定規程10~300kg/h范圍內誤差為±2%,300~3000kg/h范圍內誤差為±4%。

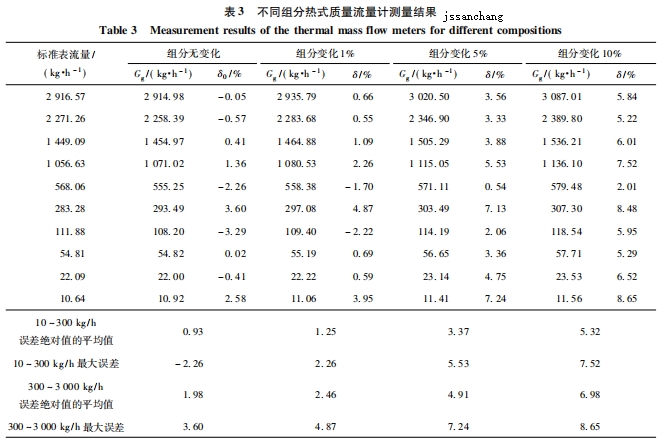
實驗的工況條件為常溫常壓,選擇空氣作為待測混合氣體,流量點選取(10~3000)kg/h的10個流量點進行測量。通過實驗對上述的計算分析進行驗證,首先,不改變組分設定進行測量,然后,通過修改了組分設定進行測量,組分設定修改依次為1%、5%、10%。不同組分設定的測量結果與誤差如表3所示。
表3中Gg表示各組分熱式流量計測量的質量流量,δ0表示未改變組分時測量的質量流量相對誤差,δ表示改變組分后測量的質量流量相對誤差。
表4為各組分的附加誤差,附加誤差表示熱式氣體質量流量計僅由于氣體組分的變化對質量流量測量的誤差,其定義式為:
3.2結果分析
由表3的實驗結果分析,組分的變化或者組分設定不準確會切實影響到質量流量的測量,并且組分變化越大,造成的質量流量的測量誤差越大。
由表4實驗結果分析,實驗的附加誤差δ'與上文計算分析的附加誤差具有很好的一致性,這使本文提出的組分變化對熱式質量流量計測量影響的定量計算公式得以驗證。
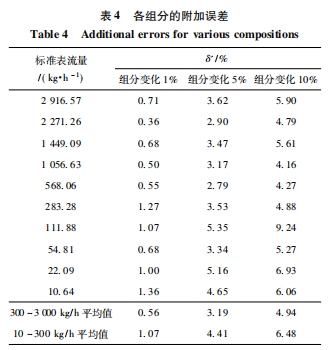
由于熱式質量流量計自身存在的誤差為2%,所以被測氣體的組分出現輕微波動時,如當組分變化1%時,對熱式質量流量計僅僅產生0.26%的附加誤差,相比較于熱式質量流量計自身的誤差,其附加誤差是相對次要的,可以忽略不計。
因此,根據表4結果分析,組分變化較大時,產生的附加誤差與熱式質量流量計自身誤差相當或更大,這種情況下由組分變化或設定不準確產生的誤差不能忽略不計。本次研究以空氣作為介質,熱式氣體質量流量計為2級的準確度等級,得出在質量流量在300~3000kg/h時,組分變化達到臨界值為3%~4%時其附加誤差大于熱式氣體質量流量計自身的誤差,進而對熱式測量造成不可忽略的影響;在質量流量在10~300kg/h時組分變化達到臨界值4~5%以上會對熱式氣體質量流量計的測量造成不可忽略的影響,這為實際工程上的應用提供了一定的借鑒。
4、結論
通過計算分析和實驗測試,本文得到以下結論:
結合熱式氣體質量流量計的換熱理論與誤差傳遞理論推導出了組分(物性參數)變化對熱式測量影響的定量關系。通過實驗進行測試,組分變化或者組分設定不準確會切實影響到質量流量的測量,且實驗結果與計算分析的附加誤差結果基本一致,使得本文提出的定量關系得以驗證,進一步確定了組分(物性參數)變化對于熱式質量流量計的測量影響。
分析并選擇了適合熱式質量流量計的各相關混合氣體物性參數計算方法。
經過實驗測試,找到了氣體組分對熱式氣體質量流量計測量產生不可忽略誤差的臨界值3~5%,組分變化超過臨界值,組分變化帶來的誤差影響大于熱式質量流量計自身的誤差影響,為實際的工程應用提供一定的參考。
作者單位:1. 天津大學電氣自動化與信息工程學院 天津 ; 2. 天津市過程檢測與控制重點實驗室 天津 300072; 3. 中國石油天然氣股份有限公司規劃總院 北京
作者簡介:
劉家旭,2018 年于河北工業大學獲得學 士學位,現為天津大學碩士研究生,主要研究方向為熱式氣體質量流量計的測量。
徐英,1992 年于吉林化工學院獲得學士 學位,1999 年和 2002 年分別于天津大學獲 得碩士和博士學位,現為天津大學教授,主 要研究方向為單相與多相流體過程參數檢 測。
張濤( 通信作者) ,1987 年于天津大學 獲得碩士學位,現為天津大學教授,主要從事流量檢測技術,智能化儀表與控制系統,傳感器與非電量測量方面的研究。
王念榕:
注明,淮安三暢儀表文章均為原創,轉載請注明本文地址http://www.58490.cn/
上一篇文章:電磁流量計在季戊四醇裝置縮臺反應中堿計量的應用
下一篇文章:渦街流量計的概念、細節和優缺點說明
相關的產品
- 商務部:推進對鼓勵外商投資項目的進口設備2023-11-18
- 蒸汽換熱站裝置儀表選型方法2023-10-19
- 在食品加工過程中泵送顆粒是否存在問題2022-03-30
- 確保精細化工行業的安全性和可持續性2022-03-30
- 超聲波流量計在天然氣計量中的應用探析2022-03-30
- 如何測量罐中兩種液體之間的界面2022-03-25













